Оценка эффективности контрольных мероприятий в кредитных организациях
![]() Риски
деятельности и ошибки являются неизбежным
следствием любого экономического процесса,
любой деятельности экономического субъекта. Чем
сложней субъект тем большее количество рисковых
событий и следовательно ошибок происходит в
каждую единицу времени. Рассматривая такой
объект исследований как кредитная организация,
авторам удалось установить ряд закономерностей,
связанных с возникновением ошибок, их
обнаружением и исправлением.
Риски
деятельности и ошибки являются неизбежным
следствием любого экономического процесса,
любой деятельности экономического субъекта. Чем
сложней субъект тем большее количество рисковых
событий и следовательно ошибок происходит в
каждую единицу времени. Рассматривая такой
объект исследований как кредитная организация,
авторам удалось установить ряд закономерностей,
связанных с возникновением ошибок, их
обнаружением и исправлением.
![]() Риски
деятельности и ошибки являются неизбежным
следствием любого экономического процесса,
любой деятельности экономического субъекта. Чем
сложней субъект тем большее количество рисковых
событий и следовательно ошибок происходит в
каждую единицу времени.
Риски
деятельности и ошибки являются неизбежным
следствием любого экономического процесса,
любой деятельности экономического субъекта. Чем
сложней субъект тем большее количество рисковых
событий и следовательно ошибок происходит в
каждую единицу времени.
![]() Рассматривая такой объект исследований как
кредитная организация, авторам удалось
установить ряд закономерностей, связанных с
возникновением ошибок, их обнаружением и
исправлением.
Рассматривая такой объект исследований как
кредитная организация, авторам удалось
установить ряд закономерностей, связанных с
возникновением ошибок, их обнаружением и
исправлением.
![]() Кредитная
организация как предмет исследования была
выбрана в связи с тем, что в её практической
деятельности существуют объекты, постоянно
подвергающиеся воздействию системы внутреннего
контроля, а так же потому, что жизненный цикл
продукта от его внедрения до получения
результатов применения
сравнительно короток. Для подтверждения
результатов исследования так же необходимо было
иметь значительное количество однородных
объектов контроля, например, такие как депозиты
населения, выданные кредитные продукты и т.д.
Кредитная
организация как предмет исследования была
выбрана в связи с тем, что в её практической
деятельности существуют объекты, постоянно
подвергающиеся воздействию системы внутреннего
контроля, а так же потому, что жизненный цикл
продукта от его внедрения до получения
результатов применения
сравнительно короток. Для подтверждения
результатов исследования так же необходимо было
иметь значительное количество однородных
объектов контроля, например, такие как депозиты
населения, выданные кредитные продукты и т.д.
![]() Следует сразу
оговориться, что предложенная модель скорее
всего может быть применима только для крупных
организаций, имеющих значительный объем
операции и широко развитую филиальную сеть и
систему внутреннего контроля. Так же одним их
необходимых условий использования данной модели
является применение автоматизированных методов
контроля, позволяющих в короткий срок проверять
значительное количество проводимых операций.
Следует сразу
оговориться, что предложенная модель скорее
всего может быть применима только для крупных
организаций, имеющих значительный объем
операции и широко развитую филиальную сеть и
систему внутреннего контроля. Так же одним их
необходимых условий использования данной модели
является применение автоматизированных методов
контроля, позволяющих в короткий срок проверять
значительное количество проводимых операций.
![]() Так как одним из
важнейших этапов развития системы внутреннего
контроля является определение эффективности
проведенных контрольных процедур, соответствия
затрат на их проведение их результатам, то данная
модель может служить одним из способов оценки
эффективности системы внутреннего контроля,
хотя и не единственным.
Так как одним из
важнейших этапов развития системы внутреннего
контроля является определение эффективности
проведенных контрольных процедур, соответствия
затрат на их проведение их результатам, то данная
модель может служить одним из способов оценки
эффективности системы внутреннего контроля,
хотя и не единственным.
![]() Мы рассмотрели
математическую модель временного процесса появления
(из-за некоторого систематического источника) и исправления
(в результате осуществления контроля) ошибок
какой-либо банковской операции.
Мы рассмотрели
математическую модель временного процесса появления
(из-за некоторого систематического источника) и исправления
(в результате осуществления контроля) ошибок
какой-либо банковской операции.
![]() Неизвестной
величиной, удовлетворяющей уравнению, является
ожидаемое (в вероятностном смысле) количество
ошибок N(t), зарегистрированных к
моменту времени t и
остающихся неисправленными. Будем полагать N(0)=0.
Уравнение для N(t) выведем постепенно в
три этапа.
Неизвестной
величиной, удовлетворяющей уравнению, является
ожидаемое (в вероятностном смысле) количество
ошибок N(t), зарегистрированных к
моменту времени t и
остающихся неисправленными. Будем полагать N(0)=0.
Уравнение для N(t) выведем постепенно в
три этапа.
1. Источник, вызывающий ошибки, будем характеризовать величиной S, равной среднему числу ошибок, возникающих за единицу времени. При наличии только источника ( и отсутствии контроля) N(t) удовлетворяет уравнению
![]() (1)
(1)
При неизменной величине источника уравнение (1) имеет очевидное решение
N(t)=S·t,
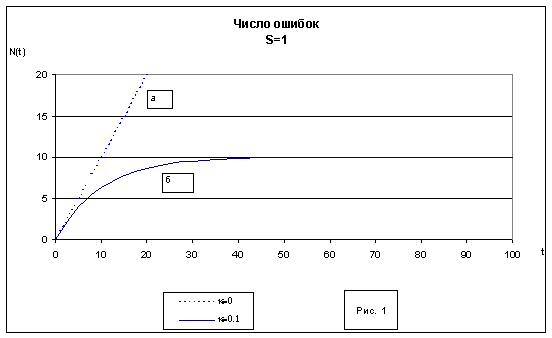
т.е. число ошибок линейно растет со временем (рис.1 а).
2. Осуществление системой внутреннего контроля контрольных процедур приводит к тому, что часть ошибок выявляется при осуществлении операций и исправляется. При этом происходит уменьшение величины N(t). Предполагая, что скорость этого уменьшения пропорциональна имеющемуся числу ошибок (это одна из возможных моделей), получим:
![]() (2)
(2)
В этой
модели действие контроля характеризуется
коэффициентом «обратной связи»
k. При неизменном
источнике S уравнение
(2) имеет следующее решение:
![]() ,
(3)
,
(3)
где e – основание натуральных логарифмов.
Число неисправленных на момент t ошибок со временем выходит на постоянное значение, равное S/k – тем меньшее, чем больше коэффициент контроля k (рис.1 б).
3. Учитывая то обстоятельство, что интенсивность источника ошибок не остается постоянной, а может уменьшаться благодаря действию контроля над правильностью выполнения операций («работа над ошибками»), т.е. S=S(t), при этом уравнение (2) имеет вид:
![]() ,
(4)
,
(4)
а его
решение дается формулой:
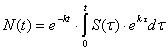 (5)
(5)
Учет возможного уменьшения функции S(t) со временем приводит к качественно новому эффекту – число ошибок N(t) после начального возрастания достигает максимума, а затем начинает убывать. Это справедливо для широкого класса функций S(t) - как с плавным (при постоянной “работе над ошибками”), так и со скачкообразным (в результате разовых мероприятий по улучшению технологии, внедрению новых контрольных процедур и т.д.) характером уменьшения.
Вначале
рассмотрим решение при резких изменениях
функции S(t),
. Введем единичную ступенчатую функцию ?(t) , равную нулю при t<0 и
единице при t>0 . Пусть источник S(t) , равный вначале S0 , затем уменьшается в моменты
времени ti на Si , таким
образом,
![]()
Подставляя
эту функцию в (5), получим следующее решение:
![]() (6)
(6)
Характер этого решения показан на рис.2. Первый член в (6) аналогичен (3), а второй «включает» в соответствующие моменты времени уменьшение числа ошибок N(t).
Теперь рассмотрим случай плавного поведения S(t). В качестве примера примем непрерывное уменьшение по экспоненциальному закону:
![]()
Коэффициент
?
показывает, насколько интенсивно происходит
уменьшение источника ошибок.
С учетом этого N(t) удовлетворяет
уравнению
![]()
которое, как следует из общей формулы (5), имеет следующее решение:
![]() .
.
Это решение по сравнению с предыдущим имеет существенную особенность: число неисправленных на момент t ошибок со временем не выходит на постоянное значение, а убывает до нуля. Это происходит из-за одновременного наличия двух факторов, действующих на уменьшение ошибок: исправления найденных ошибок («действие контроля») и уменьшения источника ошибок («работа над ошибками»).
Рассмотренная модель дает возможность определить и вычислить ряд характеристик, которые выражаются через параметры модели S0, k и ? :
t* - момент времени, при котором
число неисправленных ошибок достигает
максимума:
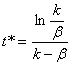
N* - максимальное значение
числа ошибок, N*=N(t*):
![]()
T -
«время жизни ошибок», т.е. момент, после которого
число ошибок резко идет на спад (экспоненциально
убывает):
![]()
I - интегральный показатель эффективности контроля - площадь под кривой N(t) – учитывающий как величину ошибок, так и время их существования:
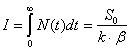
На рис.3 показана реальная зависимость N(t) для следующих параметров:
S0=1 - что соответствует появлению 1 ошибки за условную единицу времени.
k=0.1 - означает, что относительное уменьшение (исправление) ошибок за единицу времени равно 10%.
Значения ? равны 0 (источник ошибок не изменяется); 0,01 и 0,05. Соответствующие значения характеристик t*, T , N * и I указаны на рисунке, а также в таблице 1:
S0 |
k |
? |
t* |
T |
N* |
I |
1 |
0.1 |
0 |
? |
? |
10 |
? |
1 |
0.1 |
0.01 |
25.6 |
110 |
7.74 |
1000 |
1 |
0.1 |
0.05 |
13.8 |
30 |
5 |
200 |
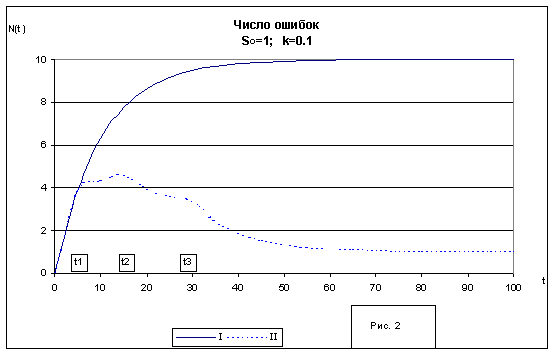
| Параметры | ||||
| Кривая I: |
S(t)=1 - не изменяется |
|||
| Кривая II: | S(t)
уменьшается скачкообразно |
|||
| в моменты
времени |
t1=5 |
t2=15 | t3=30 | |
| на величину соответственно | S1=0.5 | S2=0.2 | S3=0.2 | |
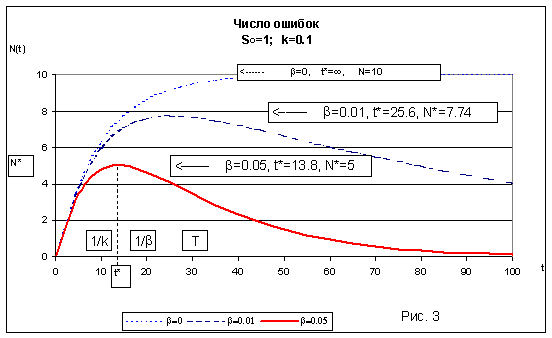
Основные характеристики |
|
| t*= ln(k/b) / (k-b) |
время, при
котором достигается максимум N |
| N*= (So/k) exp(-bt*) | максимальное
значение N |
| I= So/bk |
интегральный
показатель эффективности контроля |
| T=1/k + 1/b |
момент
начала экспоненциального спада числа ошибок |
![]() Предложенная
модель определения эффективности внутреннего
контроля должна позволить определять
эффективность различных контрольных
мероприятий составляющих систему внутреннего
контроля. Набор статистических материалов
должен определить наиболее эффективные
процедуры внутреннего контроля.
Предложенная
модель определения эффективности внутреннего
контроля должна позволить определять
эффективность различных контрольных
мероприятий составляющих систему внутреннего
контроля. Набор статистических материалов
должен определить наиболее эффективные
процедуры внутреннего контроля.
В конечном итоге данная модель должна помочь не только в оценке эффективности отдельных контрольных процедур применительно к конкретному виду банковского продукта, но и дать материалы для оценки кредитного, операционного, а так же иных видов риска в целом по кредитной организации.
(А.И. Елин, Институт внутренних аудиторов. И.К. Кобозев, к.ф.-м. н. Журнал "Контроллинг" № 3/2005 )
АИСС БКБ, www.orioncom.ru, tel (495) 783-5510